- Today
- Yesterday
- Total
메이쁘
허프만 코드(Huffman Code) 본문
허프만 코드란?
- 데이터를 효율적으로 압축하는 데 사용하는 알고리즘으로, 그리디 알고리즘에 속함.
- 데이터 빈도 수에 따라 우선순위 큐에서 작은 두 개의 노드를 꺼내고 이를 합쳐 트리를 만드는 과정이 있다.
- 고정 길이 코드와 가변 길이 코드 두 가지 표현 방법이 존재함.
허프만 코드 인코딩 과정(허프만 코드를 만드는 과정)

** 참고로 여기서 말하는 방식은 가변 길이 코드 표현 방법에 해당한다.

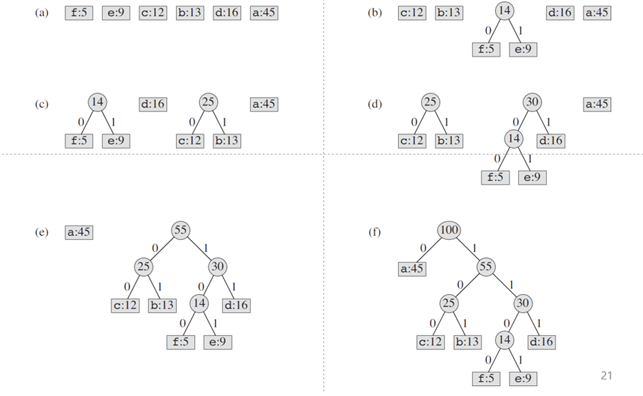
- (a) ~ (f) 까지의 과정을 담은 그림으로, 이 그림을 보면 바로 이해할 수 있을 것이다..
- (a) : 예를 들어, 인코딩을 할 문자열이 casdffsdasadceacsd 라고 주어지면, 이 문자열에 각 알파벳 별로 얼마나 포함되어있는지(빈도 수) 나타낸 수 이다.
이 수들을 우선순위 큐에 담아두고 인코딩을 시작한다.
- (b) : 가장 빈도수가 낮은 두 값(f, e)을 꺼내고 두 빈도 수를 합쳐 새로운 부모 노드를 만듬과 동시에 둘 중 낮은 빈도 수는 왼쪽, 높은 빈도 수는 오른쪽에 위치시킨다.
이 부모 노드를 다시 우선순위 큐에 넣고 이를 n - 1번 반복한다.(n은 전체 개수)
** 그 이유는
1) 두 개의 원소를 꺼내고 하나의 원소를 다시 넣기 때문이고,
2) 마지막에 큐에 남은 노드 하나가 root 노드이기 때문에 이를 리턴해서 사용해야 하기 때문이다.
인코딩 과정을 나타낸 샘플 코드
// 빈도 수를 보고 허프만 트리를 만드는 함수
public static Node huffMan(PriorityQueue<Node> q, int n) {
for(int i = 1; i < n; i++) {
Node z = new Node();
z.setLeft(q.poll());
z.setRight(q.poll());
z.setFreq(z.getLeft().getFreq() + z.getRight().getFreq()); // 빈도 수를 나타냄
q.offer(z);
}
return q.poll();
}
- 위 과정을 통해 나온 root노드(허프만 트리)의 최하위 노드들(알파벳 노드)에게 depth에 맞게 허프만 코드를 부여해줘야 함.
- 부여는 새로운 HashMap에 집어넣을 예정. 왼쪽 자식 노드는 0을, 오른쪽 자식 노드는 1을 넣으며, depth가 1씩 증가할 때마다 코드가 하나씩 뒤에 추가되어야 한다.
- 이러한 과정을 통해 얻은 HashMap을 토대로 알파벳 하나씩 허프만 코드로 인코딩한다.
- 위에 게시한 그림에서 (f)를 다시 보면 a는 0, c는 100, b는 101, d는 111, e는 1101, f는 1100이 부여된다.
** 빈도 수를 보고 코드로 바꾸는 샘플 코드
// 허프만 트리에서 빈도 수를 판단하여 코드로 바꾸는 함수
public static void getStringHuffmanCode(Node node, String str) {
if(node == null) {
return;
}
getStringHuffmanCode(node.getLeft(), str + "0"); // 좌측 노드 재귀 호출
getStringHuffmanCode(node.getRight(), str + "1"); // 우측 노드 재귀 호출
if(node.getAlphabet() != '\0') { // 빈 노드가 아닌 실제 인코딩에 사용할 알파벳이 담겨있으면 HashMap에 넣고 종료
encodedCode.put(node.getAlphabet(), str);
}
}
허프만 코드 디코딩 과정(허프만 코드를 보고 해독하는 과정)
** 참고로 허프만 테이블이 이미 있어야 함.
- 그래서 이 테이블을 허프만 트리로 고치고, 0과 1을 하나씩 읽어가면서 트리의 루트 노드부터 시작해 depth 하나씩 내려가며 존재하는 알파벳이 있는지 찾고 이를 알파벳으로 바꿔야 한다.
- 허프만 트리를 만드는 과정에서도 예를 들어, a = 1011이면 101까지는 빈 노드를 부모-자식으로 이어 붙이다가 마지막 1에 a를 넣은 노드를 만들고, 알맞은 위치에 자식 노드로 추가하고 종료한다.
- 이를 반복하여 트리를 만들고, 인코딩된 0과 1 문자에서 하나씩 보고 트리에서 depth 하나씩 0은 왼쪽 자식, 1은 오른쪽 자식 노드에 맞게 내려가며 찾는다.
디코딩 과정을 나타낸 샘플 코드
// 디코딩에 필요한 허프만 트리를 만드는 함수
public static DecodeNode makeHuffmanTree(PriorityQueue<DecodeNode> q) {
DecodeNode root = new DecodeNode(null, '-');
while(!q.isEmpty()) {
DecodeNode node = q.poll();
String code = node.getCode();
char alphabet = node.getAlphabet();
DecodeNode currentNode = root;
for(int i = 0; i < code.length() - 1; i++) { // 맨 끝 자리 수 전까지 탐색해서 노드를 만들어놓는다.
char direction = code.charAt(i);
if(direction == '0') {
if(currentNode.getLeft() == null) { // 왼쪽 자식의 노드가 널이면
currentNode = addLeftNode(currentNode, null, '-');
}
else {
currentNode = currentNode.getLeft();
}
}
if(direction == '1') {
if(currentNode.getRight() == null) { // 오른쪽 자식의 노드가 널이면
currentNode = addRightNode(currentNode, null, '-');
}
else {
currentNode = currentNode.getRight();
}
}
// addNode(direction, code, '-');
}
char direction = code.charAt(code.length() - 1); // 가장 끝 코드 문자 얻기
if(direction == '0') {
addLeftNode(currentNode, code, alphabet);
}
if(direction == '1') {
addRightNode(currentNode, code, alphabet);
}
}
return root;
}
*** 전체 코드는 깃허브에 있습니다.
'Algorithm > 알고리즘 정리' 카테고리의 다른 글
| 삽입 정렬(Insertion Sort) 에 대한 간단 정리 ! (0) | 2020.06.06 |
|---|---|
| 버블 정렬(Bubble Sort) 에 대한 간단 정리 ! (0) | 2020.06.06 |
| Union / Find Algorithm (0) | 2020.02.23 |
| 크루스칼 알고리즘(Kruskal Algorithm) (0) | 2020.02.23 |
| 벨만-포드 알고리즘(Bellman-Ford Algorithm) (0) | 2020.02.22 |


